
HL Paper 2
In beta minus (β−) decay a d quark decays into a u quark, an electron and an electron antineutrino.
Show that lepton number is conserved in this decay.
A nucleus of phosphorus-32 \(\left( {{}_{15}^{32}{\rm{P}}} \right)\) decays by beta minus (β−) decay into a nucleus of sulfur-32 \(\left( {{}_{16}^{32}{\rm{S}}} \right)\). The binding energy per nucleon of \({}_{15}^{32}{\rm{P }}\) is 8.398 MeV and for \({}_{16}^{32}{\rm{S }}\) it is 8.450 MeV.
(i) State what is meant by the binding energy of a nucleus.
(ii) Determine the energy released in this decay.
Quarks were hypothesized long before their existence was experimentally verified. Discuss the reasons why physicists developed a theory that involved quarks.
Markscheme
«lepton number on» LHS = 0 and «lepton number on» RHS = 0 +1−1
OR
quarks have no/0/zero lepton number and the lepton number for electron and the antineutrino cancel
(i)
energy released when a nucleus forms from constituent nucleons
OR
minimum energy needed/work done to break a nucleus up into its constituent nucleons
Do not allow reference to “atom”.
Award [0] for “energy to assemble nucleus”.
Do not allow “particles”, “constituents” or “components” for “nucleons”.
(ii)
«energy/mass difference =» 8.450 – 8.398 «= 0.052 MeV»
Q = 1.7 or 1.66 or 1.664 MeV
OR
2.66 × 10–13 J
quark theory is simpler OR Occam’s razor example OR simple model explains complex observations
quotes experiment that led to quark theory, eg deep inelastic scattering or electron scattering
model incorporates strong/weak interactions/forces between protons and neutrons
model incorporates conservation rules
model explains differences between neutrons and protons OR explains decay of neutron to proton
Examiners report
Rhodium-106 (\(_{\,\,\,45}^{106}{\text{Rh}}\)) decays into palladium-106 (\(_{\,\,\,46}^{106}{\text{Pd}}\)) by beta minus (β–) decay. The diagram shows some of the nuclear energy levels of rhodium-106 and palladium-106. The arrow represents the β– decay.

Bohr modified the Rutherford model by introducing the condition mvr = n\(\frac{h}{{2\pi }}\). Outline the reason for this modification.
Show that the speed v of an electron in the hydrogen atom is related to the radius r of the orbit by the expression
\[v = \sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \]
where k is the Coulomb constant.
Using the answer in (b) and (c)(i), deduce that the radius r of the electron’s orbit in the ground state of hydrogen is given by the following expression.
\[r = \frac{{{h^2}}}{{4{\pi ^2}k{m_{\text{e}}}{e^2}}}\]
Calculate the electron’s orbital radius in (c)(ii).
Explain what may be deduced about the energy of the electron in the β– decay.
Suggest why the β– decay is followed by the emission of a gamma ray photon.
Calculate the wavelength of the gamma ray photon in (d)(ii).
Markscheme
the electrons accelerate and so radiate energy
they would therefore spiral into the nucleus/atoms would be unstable
electrons have discrete/only certain energy levels
the only orbits where electrons do not radiate are those that satisfy the Bohr condition «mvr = n\(\frac{h}{{2\pi }}\)»
[3 marks]
\(\frac{{{m_{\text{e}}}{v^2}}}{r} = \frac{{k{e^2}}}{{{r^2}}}\)
OR
KE = \(\frac{1}{2}\)PE hence \(\frac{1}{2}\)mev2 = \(\frac{1}{2}\frac{{k{e^2}}}{r}\)
«solving for v to get answer»
Answer given – look for correct working
[1 mark]
combining v = \(\sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \) with mevr = \(\frac{h}{{2\pi }}\) using correct substitution
«eg \({m_e}^2\frac{{k{e^2}}}{{{m_{\text{e}}}r}}{r^2} = \frac{{{h^2}}}{{4{\pi ^2}}}\)»
correct algebraic manipulation to gain the answer
Answer given – look for correct working
Do not allow a bald statement of the answer for MP2. Some further working eg cancellation of m or r must be shown
[2 marks]
« r = \(\frac{{{{(6.63 \times {{10}^{ - 34}})}^2}}}{{4{\pi ^2} \times 8.99 \times {{10}^9} \times 9.11 \times {{10}^{ - 31}} \times {{(1.6 \times {{10}^{ - 19}})}^2}}}\)»
r = 5.3 × 10–11 «m»
[1 mark]
the energy released is 3.54 – 0.48 = 3.06 «MeV»
this is shared by the electron and the antineutrino
so the electron’s energy varies from 0 to 3.06 «MeV»
[3 marks]
the palladium nucleus emits the photon when it decays into the ground state «from the excited state»
[1 mark]
Photon energy
E = 0.48 × 106 × 1.6 × 10–19 = «7.68 × 10–14 J»
λ = «\(\frac{{hc}}{E} = \frac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{7.68 \times {{10}^{ - 14}}}}\) =» 2.6 × 10–12 «m»
Award [2] for a bald correct answer
Allow ECF from incorrect energy
[2 marks]
Examiners report
This question is about nuclear reactions.
A reaction that takes place in the core of a particular nuclear reactor is as shown.
\[_{\;92}^{235}{\text{U}} + {\text{X}} \to _{\;56}^{144}{\text{Ba}} + _{36}^{89}{\text{Kr}} + 3{\text{X}}\]
In the nuclear reactor, \(9.5 \times {10^{19}}\) fissions take place every second. Each fission gives rise to 200 MeV of energy that is available for conversion to electrical energy. The overall efficiency of the nuclear power station is 32%.
State the nature of X.
State one form of energy that is instantaneously released in the reaction.
Determine the mass of U-235 that undergoes fission in the reactor every day.
Calculate the power output of the nuclear power station.
In addition to the U-235, the nuclear reactor contains graphite that acts as a moderator. Explain the function of the moderator.
Outline how energy released in the nuclear reactor is transformed to electrical energy.
Markscheme
neutron / \(_{\text{0}}^{\text{1}}{\text{n}}\);
kinetic energy / gamma radiation / binding energy;
number of fissions in one day \( = 9.5 \times {10^{19}} \times 24 \times 3600{\text{ }}( = 8.2 \times {10^{24}})\);
mass of uranium atom \( = 235 \times 1.661 \times {10^{ - 27}}{\text{ }}( = 3.9 \times {10^{ - 25}}{\text{ kg}})\);
mass of uranium in one day \(( = 8.2 \times {10^{24}} \times 3.9 \times {10^{ - 25}}) = 3.2{\text{ kg}}\);
energy per fission \( = 200 \times {10^6} \times 1.6 \times {10^{ - 19}}{\text{ }}( = 3.2 \times {10^{ - 11}}{\text{ J}})\);
power output \( = (9.5 \times {10^{19}} \times 3.2 \times {10^{ - 11}} \times 0.32 = ){\text{ }}9.7 \times {10^8}{\text{ W}}\);
Award [1] for an answer of \(6.1 \times {10^{27}}{\text{ eV}}{{\text{s}}^{ - 1}}\).
neutrons have to be slowed down (before next fission);
because the probability of fission is (much) greater (with neutrons of thermal energy);
neutrons collide with/transfer energy to atoms/molecules (of the moderator);
kinetic energy of neutrons/thermal energy of core is transferred into thermal energy
of the coolant (and elsewhere);
(thermal energy) is converted into kinetic energy in moving steam;
(kinetic energy of steam) is transferred into (rotational) kinetic energy of turbine;
(kinetic energy of turbine) is transferred into electrical energy by dynamo/generator;
Examiners report
X is a neutron and almost all answers were correct. G2 comments suggested that the term “State the nature of X” was rather vague. This is a helpful comment, but on this occasion candidates did not seem to be affected by it.
Instantaneous energy release: Binding energy, (particle) kinetic energy, gamma radiation were all accepted. Heat energy was not accepted.
Quite a few candidates found the mass defect rather than the mass of U-235 fissioned. The mass of a Uranium atom was often incorrect – candidates were expected to determine it from the mass number. A few stated the mass as 235g. Another common error was to find mass per second, rather than per day. However many correct answers were seen.
Working was often unclear. The power station efficiency of 0.32 was often overlooked. Whilst many candidates were eventually able to determine the power output of the power station in W, there were also answers giving the energy output per day. Quite a few candidates used eV/s and this was accepted for 1 mark.
There was some confusion between a moderator and control rods. However, most candidates knew that the graphite moderator slowed neutrons (due to inelastic collisions) to thermal energies to maximise the probability of further fission.
Outlining the energy transfers occurring in a nuclear power plant is a frequent question, but answers were often poorly organised. A simple flow diagram would suffice. Thermal energy of core > thermal energy of coolant > KE of steam > KE of turbine > Electrical energy from generator, or similar. Far too many candidates barely mentioned energy; “…heat up water to make steam which turns a turbine…” gained no marks.
This question is in two parts. Part 1 is about electric fields and radioactive decay. Part 2 is about waves.
Part 1 Electric fields and radioactive decay
An ionization chamber is a device which can be used to detect charged particles.
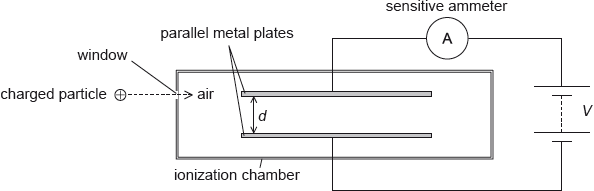
The charged particles enter the chamber through a thin window. They then ionize the air between the parallel metal plates. A high potential difference across the plates creates an electric field that causes the ions to move towards the plates. Charge now flows around the circuit and a current is detected by the sensitive ammeter.
The separation of the plates d is 12 mm and the potential difference \(V\) between the plates is 5.2 kV. An ionized air molecule M with charge \( + 2e\) is produced when a charged particle collides with an air molecule.
Radium-226 \({\text{(}}_{\;{\text{88}}}^{{\text{226}}}{\text{Ra)}}\) decays into an isotope of radon (Rn) by the emission of an alpha particle and a gamma-ray photon. The alpha particle may be detected using the ionization chamber but the gamma-ray photon is unlikely to be detected.
On the diagram, draw the shape of the electric field between the plates.
Calculate the electric field strength between the plates.
Calculate the force on M.
Determine the change in the electric potential energy of M as it moves from the positive to the negative plate.
Construct the nuclear equation for the decay of radium-226.
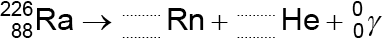
Radium-226 has a half-life of 1600 years. Determine the time, in years, it takes for the activity of radium-226 to fall to 5% of its original activity.
Markscheme
minimum of three lines equally spaced and distributed, perpendicular to the plates and downwards; edge effect shown; } (condone lines that do not touch plates)
\(4.3 \times {10^5}{\text{ (N}}{{\text{C}}^{ - 1}}{\text{)}}\)
\((F = Eq = ){\text{ }}4.3 \times {10^5} \times 2 \times 1.6 \times {10^{ - 19}}\); (allow ECF from (b)(i))
\(1.4 \times {10^{ - 13}}{\text{ (N)}}\);
Award [2] for a bald correct answer.
\(\Delta {E_{\text{P}}} = q\Delta V\)\(\,\,\,\)or\(\,\,\,\)\(3.2 \times {10^{ - 19}} \times 5.2 \times {10^3}\);
\(1.7 \times {10^{ - 15}}{\text{ (J)}}\);
negative/loss;
\(\left( {_{\;88}^{226}{\text{Ra}} \to _{\;86}^{222}{\text{Rn}} + _2^4{\text{He}} + _0^0\gamma } \right)\)
\(_{\;86}^{222}{\text{Rn}}\)\(\,\,\,\)or\(\,\,\,\)\(_2^4{\text{He}}\);
numbers balance top and bottom on right-hand side;
\(\lambda = \frac{{\ln 2}}{{1600}} = 4.33 \times {10^{ - 4}}{\text{ (y}}{{\text{r}}^{ - 1}}{\text{)}}\);
\(0.05 = {{\text{e}}^{ - \lambda t}}\);
6900 (years);
Award [3] for a bald correct answer.
Award [2 max] for 2.18 \( \times \) 1011 (s).
Award [1 max] to a candidate who identifies time as about 4.3 half-lives but cannot get further or gives an approximate reasoned answer.
However award [3] if number n of half-lives is calculated from 0.05 = 2–n (= 4.32 usually from use of log2 working) and time shown.
Examiners report
Field patterns were often negligently drawn. Lines did not meet both plates, edge effects were ignored, and the (vital) equality of spacing between drawn lines was not considered. Candidates continue to show their inadequacy in responding to questions that demand a careful and accurate diagram.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part.
This sequence of calculations was often undertaken well with appropriate figures carried through from part to part. The only common error was the omission of a consideration of the gain or loss of the energy change in part (iii).
As one of the easiest questions on the paper this was predictably well done.
In the past candidates have found calculation involving exponential change difficult. On this occasion, however examiners saw a large number of correct and well explained solutions from candidates.
This question is about nuclear processes.
Describe what is meant by
(i) radioactive decay.
(ii) nuclear fusion.
Tritium is a radioactive nuclide with a half-life of 4500 days. It decays to an isotope of helium.
Determine the time taken for 90% of a sample of tritium to decay.
A nuclide of deuterium \(\left( {{}_1^2{\rm{H}}} \right)\) and a nuclide of tritium \(\left( {{}_1^3{\rm{H}}} \right)\) undergo nuclear fusion. The reaction equation for this process is
\[{}_1^2{\rm{H + }}{}_1^3{\rm{H}} \to {}_2^4{\rm{He + X}}\]
Identify X.
Markscheme
(i) refers to unstable nucleus/isotope / refers to spontaneous/random process;
which emits named radiation (from nucleus) / forms different nucleus/isotope;
(ii) combination of two nuclei / OWTTE; (do not allow “particles” or “atoms”)
to form new nuclide with greater mass/larger nucleus/greater number of nucleons;
\(\lambda = \frac{{\ln 2}}{{4500}}\left( { = 1.54 \times {{10}^{ - 4}}} \right)\);
\(0.1{N_0} = {N_0}{{\rm{e}}^{ - 1.54 \times {{10}^{ - 4}}t}}\);
1.5×104(d) or 1.3×109(s);
Award [2 max] if answer is time to lose 10% (680 d).
Allow answer to be expressed in any time units.
Award [3] for a bald correct answer.
or
\(\ln 0.1 = \frac{{ - 0.69t}}{{{t_{\frac{1}{2}}}}}\);
t=3.3×4500;
1.5×104(d);
Award [2 max] if answer is time to lose 10% (680 d).
Allow answer to be expressed in any time units.
Award [3] for a bald correct answer.
\({}_0^1n\)/neutron;
Examiners report
This question is about the Rutherford model of the atom.
The isotope gold-197 \(\left( {_{\;{\text{79}}}^{{\text{197}}}{\text{Au}}} \right)\) is stable but the isotope gold-199 \(_{\;{\text{79}}}^{{\text{199}}}{\text{Au}}\) is not.
A nucleus of \(_{\;{\text{79}}}^{{\text{199}}}{\text{Au}}\) decays to a nucleus of \(_{\;{\text{80}}}^{{\text{199}}}{\text{Hg}}\). State the two particles, other than \(\gamma \)-photon, emitted in this decay.
Markscheme
electron/beta (condone lack of sign);
anti neutrino / \(\bar v\);
Allow undefined symbols if unambiguous.
Examiners report
Most candidates could write with confidence about the repulsive nature of the proton-proton interaction and the attractive nature of the strong nuclear force. Few gave good accounts of the balance between these two forces or described the energy situation (a better way to answer). Weak candidates could not name the strong nuclear force adequately.
This question is about binding energy and mass defect.
(i) The nuclear mass of the nuclide helium-3 \(\left( {_2^3{\text{He}}} \right)\) is 3.014931 u. Show that the binding energy per nucleon for the nuclide is about 2.6 MeV.
(ii) The binding energy per nucleon for deuterium \(\left( {_1^2{\text{H}}} \right)\) is 1.11 MeV. Calculate the energy change in the following reaction.
\[_1^2{\text{H}} + _1^1{\text{H}} \to _2^3{\text{HE}} + \gamma \]
(iii) The cross on the grid shows the binding energy per nucleon and nucleon number A of the nuclide nickel-62.

On the grid, sketch a graph to show how the average binding energy per nucleon varies with nucleon number A.
(iv) State and explain, with reference to your sketch graph, whether energy is released or absorbed in the reaction in (b)(ii).
Markscheme
(i) mass defect \(\left( {[2 \times 1.007276 + 1.008665] - 3.014931 = } \right){\text{ }}0.008286{\text{ u}}\);
binding energy per nucleon \(\left( {\frac{{0.008286 \times 931.5}}{3} = } \right)\frac{{7.7}}{3}\)\(\,\,\,\)or\(\,\,\,\)\(2.58{\text{ (MeV)}}\);
(ii) binding energy of left-hand side \( = 1.11 \times 2\) and binding energy of right-hand side \( = 3 \times 2.6\); } (both needed) (allow ECF)
energy release \( = 5.58{\text{ (MeV)}}\); (ignore sign)
(iii) line goes through Ni point and nickel is the maximum ±2 small squares horizontally; } (allow Fe-56 as maximum – this is just outside the range allowed)
line starts at 0, downward trend for A after 62, trend after nickel less steep than before;
Line must go through part of the X to award first marking point.
Line must not flatten out to award second marking point.
Allow smooth curve for low A.
Allow incorrect variations at low A.
(iv) nucleus produced in the reaction is higher up the curve than the reactants / OWTTE; } (must see reference to graph)
reference to binding energy/other valid reason results in energy release;
Award [0] for a bald correct answer.
Award [0] for any discussion of fission.
Examiners report
(i) This relatively easy problem was not well done. There were many permutations of the numbers, and almost all were poorly explained. Completely correct solutions were rare and even these tended to have a poor level of explanation.
(iii) Candidates are required to be able to draw and annotate this plot. This question proved that very many do not appreciate the prominent features. There were mis-drawings on both sides of the maximum; the maximum itself was often misplaced by more than the specified tolerance (showing that candidates do not appreciate the minimum value of the binding energy per nucleon at the Fe-56 or Ni position). Other errors included inappropriate gradients on the right-hand side of the graph compared to the left and failures to begin the curve at the correct place.
(iv) Few candidates referred their knowledge to the graph and simply recalled – often correctly – some physics about the stability of the fusion product. However, this was rarely referred to the relative position of reactants and product on the graph.
Part 2 Energy levels of the hydrogen atom
The diagram represents the three principal spectral lines in the visible region of the spectrum of atomic hydrogen.
The electron in the hydrogen atom can only occupy certain allowed energy levels.
(i) Outline how the spectral lines provide evidence for the existence of these energy levels.
(ii) Determine the difference in energy between the two levels from which electron transitions give rise to the Hα and Hγ spectral lines respectively.
Markscheme
(i) spectral lines are discrete;
therefore energy of photon is discrete/quantized;
photon energy is equivalent to difference in energy that electron has in each (discrete) level / ΔE = hf / OWTTE;
(so electron levels are themselves discrete)
(ii) difference in energy = \(hc\left[ {\frac{1}{{{\lambda _\gamma }}} - \frac{1}{{{\lambda _\alpha }}}} \right]\);
=6.6×10-34×3×108×107×0.0780=1.54×10-19J;
or
\({E_\alpha } = \left[ {\frac{{hc}}{{{\lambda _\alpha }}}} \right] = \frac{{6.6 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{6.56 \times {{10}^{ - 7}}}} = 3.02 \times {10^{ - 19}}{\rm{J}}\) or 1.89eV
\({E_\gamma } = \left[ {\frac{{hc}}{{{\lambda _\gamma }}}} \right] = \frac{{6.6 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{4.34 \times {{10}^{ - 7}}}} = 4.56 \times {10^{ - 19}}{\rm{J}}\) or 2.85eV {(both needed for the mark)
difference in energy=1.54×10-19J or 0.963 eV;
Examiners report
(i) Although a good chain of argument was seen from many, some candidates struggled to relate the diagram to the existence of energy levels. Sometimes this resulted in a description of photon release that was accurate but irrelevant.
(ii) Simple algebraic misconceptions prevented many from obtaining a correct solution. It was common to see a subtraction of the values of the two wavelengths rather than a subtraction of the reciprocals. Candidates who carried both energies through separately scored more highly than those who attempted early subtractions.
Part 3 Atomic energy levels
Outline how atomic emission spectra provide evidence for the quantization of energy in atoms.
Consider an electron confined in a one-dimensional “box” of length L. The de Broglie waves associated with the electron are standing waves with wavelengths given by \(\frac{{2L}}{n}\), where n=1, 2, 3, …
Show that the energy En of the electron is given by
\[En = \frac{{{n^2}{h^2}}}{{8{m_e}{L^2}}}\]
where h is Planck’s constant and me is the mass of the electron.
An electron is confined in a “box” of length L=1.0×10–10m in the n=1 energy level. Its position as measured from one end of the box is (0.5±0.5)×10–10m. Determine
(i) the momentum of the electron.
(ii) the uncertainty in the momentum.
Markscheme
all particles have an associated wavelength / OWTTE;
wavelength is given by \(\lambda = \frac{h}{p}\), where h is Planck’s constant and p is momentum;
from de Broglie hypothesis, \({p_n} = \frac{h}{{{\lambda _n}}} = \frac{{nh}}{{2L}}\);
kinetic energy given by \({E_K} = \frac{{{p^2}}}{{2{m_e}}}\);
combined and manipulated to obtain result;
(i) \(\lambda = \frac{{2L}}{n} = \frac{{2 \times 1.0 \times {{10}^{ - 10}}}}{1} = 2.0 \times {10^{ - 10}}\);
\(p = \frac{h}{\lambda } = \frac{{6.6 \times {{10}^{ - 34}}}}{{2.0 \times {{10}^{ - 10}}}} = 3.3 \times {10^{ - 24}}{\rm{kgm}}{{\rm{s}}^{ - 1}}\);
Award [2] for alternative methods, e.g. calculating energy then momentum.
(ii) use of \(\Delta x\Delta p \ge \frac{h}{{4\pi }}\);
to get \(\Delta p \ge \frac{{6.6 \times {{10}^{ - 34}}}}{{4\pi \times 0.5 \times {{10}^{ - 10}}}} = 1.1 \times {10^{ - 24}}{\rm{kgm}}{{\rm{s}}^{ - 1}}\);
Examiners report
A particular K meson has a quark structure \({\rm{\bar u}}\)s. State the charge, strangeness and baryon number for this meson.
The Feynman diagram shows the changes that occur during beta minus (β–) decay.
Label the diagram by inserting the four missing particle symbols and the direction of the arrows for the decay particles.
C-14 decay is used to estimate the age of an old dead tree. The activity of C-14 in the dead tree is determined to have fallen to 21% of its original value. C-14 has a half-life of 5700 years.
(i) Explain why the activity of C-14 in the dead tree decreases with time.
(ii) Calculate, in years, the age of the dead tree. Give your answer to an appropriate number of significant figures.
Markscheme
charge: –1«e» or negative or K−
strangeness: –1
baryon number: 0
Negative signs required.
Award [2] for three correct answers, [1 max] for two correct answer and [0] for one correct answer.
correct symbols for both missing quarks
exchange particle and electron labelled W or W– and e or e–
Do not allow W+ or e+ or β+. Allow β or β–.
arrows for both electron and anti-neutrino correct
Allow ECF from previous marking point.
i
number of C-14 atoms/nuclei are decreasing
OR
decreasing activity proportional to number of C-14 atoms/nuclei
OR
A = A0e–λt so A decreases as t increases
Do not allow “particles”
Must see reference to atoms or nuclei or an equation, just “C-14 is decreasing” is not enough.
ii
0.21 = (0.5)n
OR
\(0.21 = {e^{ - \left( {\frac{{\ln 2 \times t}}{{5700}}} \right)}}\)
n = 2.252 half-lives or t =1 2834 «y»
Early rounding to 2.25 gives 12825 y
13000 y rounded correctly to two significant figures:
Both needed; answer must be in year for MP3.
Allow ECF from MP2.
Award [3] for a bald correct answer.
Examiners report
The first scientists to identify alpha particles by a direct method were Rutherford and Royds. They knew that radium-226 (\({}_{86}^{226}{\text{Ra}}\)) decays by alpha emission to form a nuclide known as radon (Rn).
At the start of the experiment, Rutherford and Royds put 6.2 x 10–4 mol of pure radium-226 in a small closed cylinder A. Cylinder A is fixed in the centre of a larger closed cylinder B.
The experiment lasted for 6 days. The decay constant of radium-226 is 1.4 x 10–11 s–1.
At the start of the experiment, all the air was removed from cylinder B. The alpha particles combined with electrons as they moved through the wall of cylinder A to form helium gas in cylinder B.
Write down the nuclear equation for this decay.
Deduce that the activity of the radium-226 is almost constant during the experiment.
Show that about 3 x 1015 alpha particles are emitted by the radium-226 in 6 days.
The wall of cylinder A is made from glass. Outline why this glass wall had to be very thin.
The experiment was carried out at a temperature of 18 °C. The volume of cylinder B was 1.3 x 10–5 m3 and the volume of cylinder A was negligible. Calculate the pressure of the helium gas that was collected in cylinder B over the 6 day period. Helium is a monatomic gas.
Markscheme
\(_2^4\alpha \)
OR
\({}_2^4{\text{He}}\)
\({}_{86}^{222}{\text{Rn}}\)
These must be seen on the right-hand side of the equation.
ALTERNATIVE 1
6 days is 5.18 x 105 s
activity after 6 days is \({A_0}{e^{ - 1.4 \times {{10}^{ - 11}} \times 5.8 \times {{10}^5}}} \approx {A_0}\)
OR
A = 0.9999927 A0 or 0.9999927 \(\lambda \)N0
OR
states that index of e is so small that \(\frac{A}{{{A_0}}}\) is ≈ 1
OR
A – A0 ≈ 10–15 «s–1»
ALTERNATIVE 2
shows half-life of the order of 1011 s or 5.0 x 1010 s
converts this to year «1600 y» or days and states half-life much longer than experiment compared to experiment
Award [1 max] if calculations/substitutions have numerical slips but would lead to correct deduction.
eg: failure to convert 6 days to seconds but correct substitution into equation will give MP2.
Allow working in days, but for MP1 must see conversion of \(\lambda \) or half-life to day–1.
ALTERNATIVE 1
use of A = \(\lambda \)N0
conversion to number of molecules = nNA = 3.7 x 1020
OR
initial activity = 5.2 x 109 «s–1»
number emitted = (6 x 24 x 3600) x 1.4 x 10–11 x 3.7 x 1020 or 2.7 x 1015 alpha particles
ALTERNATIVE 2
use of N = N0\({e^{ - \lambda t}}\)
N0 = n x NA = 3.7 x 1020
alpha particles emitted «= number of atoms disintegrated = N – N0 =» N0\(\left( {1 - {e^{ - \lambda \times 6 \times 24 \times 3600}}} \right)\) or 2.7 x 1015 alpha particles
Must see correct substitution or answer to 2+ sf for MP3
alpha particles highly ionizing
OR
alpha particles have a low penetration power
OR
thin glass increases probability of alpha crossing glass
OR
decreases probability of alpha striking atom/nucleus/molecule
Do not allow reference to tunnelling.
conversion of temperature to 291 K
p = 4.5 x 10–9 x 8.31 x «\(\frac{{291}}{{1.3 \times {{10}^{ - 5}}}}\)»
OR
p = 2.7 x 1015 x 1.3 x 10–23 x «\(\frac{{291}}{{1.3 \times {{10}^{ - 5}}}}\)»
0.83 or 0.84 «Pa»
Allow ECF for 2.7 x 1015 from (b)(ii).
Examiners report
This question is in two parts. Part 1 is about simple harmonic motion (SHM) and waves. Part 2 is about atomic and nuclear energy levels.
Part 1 Simple harmonic motion (SHM) and waves
Part 2 Atomic and nuclear energy levels
A particle P moves with simple harmonic motion.
(i) State, with reference to the motion of P, what is meant by simple harmonic motion.
(ii) State the phase difference between the displacement and the velocity of P.
The diagram shows four spectral lines in the visible line emission spectrum of atomic hydrogen.
(i) Outline how such a spectrum may be obtained in the laboratory.
(ii) Explain how such spectra give evidence for the existence of discrete atomic energy levels.
The energies of the principal energy levels in atomic hydrogen measured in eV are given by the expression
\({E_n} = - \frac{{13.6}}{{{n^2}}}\) where n=1, 2, 3 ..........
The visible lines in the spectrum correspond to electron transitions that end at n=2.
(i) Calculate the energy of the level corresponding to n=2.
(ii) Show that the spectral line of wavelength λ=485nm is the result of an electron transition from n=4.
The alpha particles and gamma rays produced in radioactive decay have discrete energy spectra. This suggests that nuclei also possess discrete energy levels. However, beta particles produced in radioactive decay have continuous energy spectra. Describe how the existence of the antineutrino accounts for the continuous nature of beta spectra.
Markscheme
(i) the acceleration (of a particle/P) is (directly) proportional to displacement;
and is directed towards equilibrium/in the opposite direction to displacement;
Do not accept “directed towards the centre”.
(ii) \(\frac{\pi }{2}\)/90°/quarter of a period;
(i) light from a hydrogen discharge tube/hot hydrogen gas/ hydrogen tube with potential difference across it;
is passed onto a prism/diffraction grating;
and then is observed on a screen/through a telescope;
Accept good labelled diagram for explanation of any marking point.
(ii) each wavelength corresponds to the energy of the photon emitted;
when an electron makes a transition from a higher to lower energy level;
since only discrete wavelengths/finite number of wavelengths are present, then only discrete energy levels are present / OWTTE;
(i) −3.40 eV;
Award [0] for omitted negative sign.
(ii) energy difference between levels\( = \frac{{hc}}{{\lambda e}} = \frac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{4.85 \times {{10}^{ - 7}} \times 1.6 \times {{10}^{ - 19}}}}\);
=2.55eV;
\(\left[ {3.40 - 2.55} \right] = 0.85 = \frac{{13.6}}{{{n^2}}}\) to give n2=16;
n=4;
Award [3] for reversed argument.
the total emitted energy is shared between the electron and the antineutrino;
the energy/velocity can be shared/distributed in an infinite number of ways / OWTTE;
Examiners report
Part 2 Atomic spectra
The diagram shows some of the principal energy levels of atomic hydrogen.
The emission line spectrum of atomic hydrogen contains a blue line of wavelength 490nm.
(i) Calculate, in eV, the energy of a photon of wavelength 490 nm.
(ii) On the diagram above, identify with an arrow, the electron transition that gives rise to the emission line of wavelength 490 nm.
Markscheme
(i) \(\frac{{6.7 \times {{10}^{ - 34}} \times 3.0 \times {{10}^8}}}{{4.9 \times {{10}^{ - 7}}}}\);
2.5 or 2.6 eV;
(ii) transition between –0.85 and –3.4;
correct direction of arrow (down);
Examiners report
The Feynman diagram shows electron capture.
Particles can be used in scattering experiments to estimate nuclear sizes.
Electron diffraction experiments indicate that the nuclear radius of carbon-12 is 2.7 x 10–15 m. The graph shows the variation of nuclear radius with nucleon number. The nuclear radius of the carbon-12 is shown on the graph.
State and explain the nature of the particle labelled X.
Outline how these experiments are carried out.
Outline why the particles must be accelerated to high energies in scattering experiments.
State and explain one example of a scientific analogy.
Determine the radius of the magnesium-24 nucleus.
Plot the position of magnesium-24 on the graph.
Draw a line on the graph, to show the variation of nuclear radius with nucleon number.
Markscheme
«electron» neutrino
it has a lepton number of 1 «as lepton number is conserved»
it has a charge of zero/is neutral «as charge is conserved»
OR
it has a baryon number of 0 «as baryon number is conserved»
Do not allow antineutrino
Do not credit answers referring to energy
«high energy particles incident on» thin sample
detect angle/position of deflected particles
reference to interference/diffraction/minimum/maximum/numbers of particles
Allow “foil” instead of thin
λ \( \propto \frac{1}{{\sqrt E }}\) OR λ \( \propto \frac{1}{E}\)
so high energy gives small λ
to match the small nuclear size
Alternative 2
E = hf/energy is proportional to frequency
frequency is inversely proportional to wavelength/c = fλ
to match the small nuclear size
Alternative 3
higher energy means closer approach to nucleus
to overcome the repulsive force from the nucleus
so greater precision in measurement of the size of the nucleus
Accept inversely proportional
Only allow marks awarded from one alternative
two analogous situations stated
one element of the analogy equated to an element of physics
eg: moving away from Earth is like climbing a hill where the contours correspond to the equipotentials
Atoms in an ideal gas behave like pool balls
The forces between them only act during collisions
R = 2.7 x 10–15 x \({2^{\frac{1}{3}}}\)
3.4 – 3.5 x 10–15 «m»
Allow use of the Fermi radius from the data booklet
correctly plotted
Allow ECF from (d)(i)
single smooth curve passing through both points with decreasing gradient
through origin
Examiners report
The radioactive nuclide beryllium-10 (Be-10) undergoes beta minus (β–) decay to form a stable boron (B) nuclide.
The initial number of nuclei in a pure sample of beryllium-10 is N0. The graph shows how the number of remaining beryllium nuclei in the sample varies with time.
An ice sample is moved to a laboratory for analysis. The temperature of the sample is –20 °C.
Identify the missing information for this decay.
Beryllium-10 is used to investigate ice samples from Antarctica. A sample of ice initially contains 7.6 × 1011 atoms of beryllium-10. The present activity of the sample is 8.0 × 10−3 Bq.
Determine, in years, the age of the sample.
The temperature in the laboratory is higher than the temperature of the ice sample. Describe one other energy transfer that occurs between the ice sample and the laboratory.
Markscheme
\(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}} \to _{{\mkern 1mu} {\mkern 1mu} 5}^{10}{\text{B}} + _{ - 1}^{\,\,\,0}{\text{e}} + {\overline {\text{V}} _{\text{e}}}\)
antineutrino AND charge AND mass number of electron \(_{ - 1}^{\,\,\,0}{\text{e}}\), \(\overline {\text{V}} \)
conservation of mass number AND charge \(_{\,\,5}^{10}{\text{B}}\), \(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}}\)
Do not accept V.
Accept \({\bar V}\) without subscript e.
[2 marks]
λ «= \(\frac{{\ln 2}}{{1.4 \times {{10}^6}}}\)» = 4.95 × 10–7 «y–1»
rearranging of A = λN0e–λt to give –λt = ln \(\frac{{8.0 \times {{10}^{-3}} \times 365 \times 24 \times 60 \times 60}}{{4.95 \times {{10}^{-7}} \times 7.6 \times {{10}^{11}}}}\) «= –0.400»
t = \(\frac{{ - 0.400}}{{ - 4.95 \times {{10}^{ - 7}}}} = 8.1 \times {10^5}\) «y»
Allow ECF from MP1
[3 marks]
from the laboratory to the sample
conduction – contact between ice and lab surface.
OR
convection – movement of air currents
Must clearly see direction of energy transfer for MP1.
Must see more than just words “conduction” or “convection” for MP2.
[2 marks]
Examiners report
Part 2 Radioactivity
Radium-224 \(\left( {{}_{88}^{224}{\rm{RA}}} \right)\) is a radioactive nuclide that decays to form radon-220. Radon-220 is itself radioactive and undergoes a further decay. The table shows the series of radioactive nuclides that are formed as the decays proceed. The series ends with a stable isotope of lead.
For the final thallium nuclide, identify the
(i) nucleon number.
(ii) proton number.
Radon-220 is a radioactive gas. It is released by rocks such as granite. In some parts of the world, houses are built from materials containing granite. Explain why it is unlikely that radon-220 will build up in sufficient quantity to be harmful in these houses.
(i) Calculate, in hour−1, the decay constant of lead-212.
(ii) In a pure sample of lead-212 at one instant, 8.0 × 10−3 kg of the lead-212 is present. Calculate the mass of lead-212 that remains after a period of 35 hours.
(iii) A sample of pure radium begins to decay by the series shown in the table. At one instant, a mass of 8.0 × 10−3 kg of lead-212 is present in the sample. Suggest why, after 35 hours, there will be a greater mass of lead-212 present in the sample than the value you calculated in (h)(ii).
Markscheme
(i) 208;
(ii) 81;
because the half-life is (only) 55 s;
radon is produced slowly but decays quickly (so cannot build up);
(i) \(\left( {\lambda = \frac{{{\rm{In2}}}}{{{{\rm{T}}_{\frac{1}{2}}}}} = \frac{{0.693}}{{10.6}} = } \right)6.5 \times {10^{ - 2}}{\rm{ hou}}{{\rm{r}}^{ - 1}}\)
(ii) use of λ from (h)(i);
correct substitution into N = N0e−λt ;
8.0 to 8.3 × 10–4 kg;
(iii) the rate of decay/activity of polonium/radium;
is greater than the rate of decay/activity of lead;